lean-kg
An interactive dependency graph of mathlib4.
GitHub: https://github.com/rjain2470/lean-kg.
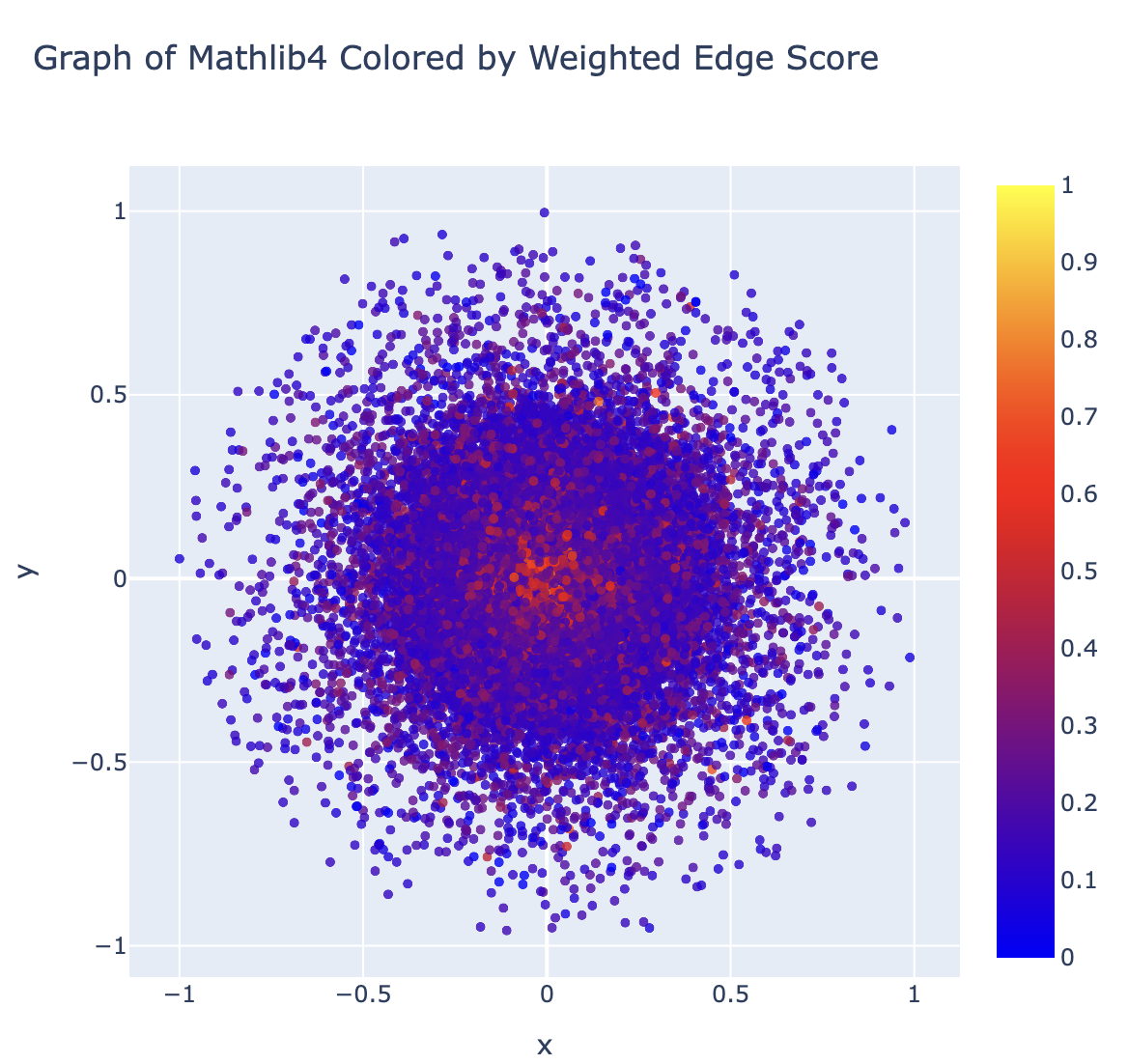
Interactive sample dependency graph of mathlib4 (20k nodes). Click on the image to explore!
LeanKG is a Python library designed to generate and visualize the dependency graph of the collection of theorems formalized in Lean. It constructs the graph as follows:
- First, LeanKG traverses the directory tree of Mathlib4 to identify all .lean files. It then reads each file and extracts the dependencies between modules, definitions, and theorems using keywords. Namespace contexts like open and namespace are dynamically resolved to ensure accurate identification of dependencies.
- Using the extracted dependencies, Lean-KG constructs a directed multigraph with the
networkxlibrary. Nodes in the graph represent declarations (such as theorems, definitions, axioms), while edges capture the dependency relationships between them. Additional metadata, such as the type of declaration (constructor, axiom, theorem, etc.), is embedded in each node for better analysis. - For visualization purposes, we can sample and plot a subgraph in 2D space using
networkx’s inbuiltspring_layout()function. Here, each node $N$ is colored according to a custom connectivity score $C(N)$, where $C(N)$ is the approximate normalization of the sum \(\sum_{k=1}^{\infty} \frac{1}{2^{f(N,k)}},\) and $f(N,k)$ is the number of nodes connected to $N$ by a sequence of edges of length $k$. - For further analysis, we can optionally convert our graph into a so-called knowledge graph, and, choosing an embedding model from the
PYKEENlibrary, embed our graph into high-dimensional Euclidean space. This embedding will group nodes with high amounts of codependency close together, and vice versa. - From here, we can input any pair of formal theorems/statements in mathlib4, and, based on the embedding, obtain a “probability” that the two are directly linked. Moreover, we can search the graph for “missing links”, i.e. we can search for pairs of theorems which are not directly linked, yet have a high probability of being linked.
In essence, Lean-KG provides a comprehensive, dependency-aware embedding framework for mathlib4, both for visualization in 2D space, and for analysis in higher dimensions.
Limitations
Since the extraction of dependencies is based on syntax, Lean-KG may overlook certain dependencies and struggle with complex file structures. Moreover, the quality of the embeddings generated by PYKEEN depend highly on the embedding hyperparameters, e.g. the choice of the embedding model and the number of epochs for training. Finally, as the Lean-KG’a embedding features depend on networkx and PYKEEN, any limitations applying to these two libraries also apply to Lean-KG.