rag-prover

GitHub: https://github.com/rjain2470/rag-prover.

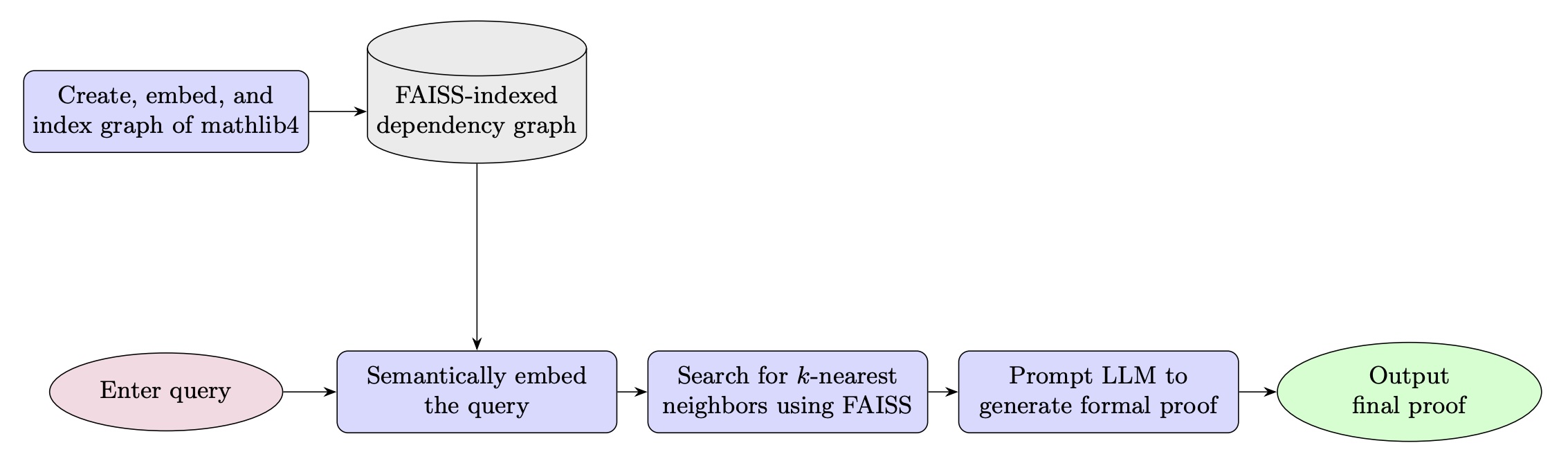
Diagram of RAG-prover’s workflow.

RAG-prover is Retrieval-Augmented Generation (RAG)-based autoreasoning model, designed to automatically generate formal proofs in Lean. Built atop DeepSeek-Prover-V2 7B, a lightweight LLM designed for autoformalization, RAG-prover implements semantic retrieval to bolster the performance of the underlying model.

Workflow

The workflow of RAG-prover consists of the following key steps:

• To start, RAG-prover preprocesses mathlib4, a massive collection of over 100k formal theorems and proofs, into a collection of vectors in high-dimensional Euclidean space. In particular, it uses OpenAI’s text-embedding-3-large to embed the library into $\mathbb{R}^n$, grouping semantically similar files together. Then, the resulting embeddings are indexed using FAISS, allowing for efficient approximate-nearest-neighbors (ANN) search. Due to the computational complexity of these tasks, this embedding is precomputed, and can be loaded by the user.

• The user begins the workflow by inputting a query (a formal or informal mathematical statement), and a parameter $k$.

• Then, using text-embedding-3-large, RAG-prover semantically embeds this query, retrieves its approximate $k$-nearest neighbors, and prompts DeepSeek-Prover to provide a formal proof conditioned on the query and the retrieved context. Then, it returns the output.

Key Features

1. RAG Architecture: By using Retrieval-Augmented Generation and providing the names of real, relevant mathlib files, we effectively mitigate the tendency of LLMs to hallucinate file names, therefore improving accuracy.
2. Scalability and Low Computational Cost: RAG-prover utilizes recent advances in efficient vector search such as FAISS to improve the capabilities of the underlying LLM with only a small addition to computational cost.

Example

Let us demonstate how RAG-prover works with an example. Suppose we input the query

∀ n m : ℕ, n + m = m + n

with $k=5$. After semantically embedding our query, RAG-prover constructs the following prompt for DeepSeek-Prover-V2:

You are an expert Lean 4 code generator. Your goal is to prove the following statement:
STATEMENT:
∀ n m : ℕ, n + m = m + n

You may find the following list of theorems/formal statements helpful:
• Logic.Equiv.Fin.Basic.finAddFlip : Fin (m + n) ≃ Fin (n + m)
• Data.Nat.Init.dvd_right_iff_eq : (∀ a : ℕ, m ∣ a ↔ n ∣ a) ↔ m = n
• Data.Nat.Init.dvd_left_iff_eq : (∀ a : ℕ, a ∣ m ↔ a ∣ n) ↔ m = n
• Algebra.Group.Int.Even.even_sub : Even (m - n) ↔ (Even m ↔ Even n)
• Data.ENat.Basic.forall_natCast_le_iff_le : (∀ a : ℕ, a ≤ m → a ≤ n) ↔ m ≤ n

Before producing the Lean 4 code to formally prove the given theorem, provide a detailed proof plan 
outlining the main proof steps and strategies. The plan should highlight key ideas, intermediate 
lemmas, and proof structures that will guide the construction of the final formal proof.

After some reasoning, the model produces the following, correct formal proof in Lean:

1
2
3
4
5
6
7
8
9
10
11
12
13
 
theorem statement : ∀ n m : ℕ, n + m = m + n := by
  have h_main : ∀ n m : ℕ, n + m = m + n := by
    intro n
    intro m
    induction m with
    | zero =>
      -- Base case: m = 0
      simp
    | succ m ih =>
      -- Inductive step: assume the statement holds for m, prove for m + 1
      simp_all [Nat.add_assoc, Nat.add_comm, Nat.add_left_comm]
      <;> omega
  exact h_main
 

Limitations

While RAG-prover provides an enhancement of DeepSeek-Prover-V2, it also has several limitations. For one, it does not currently include compiler feedback, meaning that correct output is not guaranteed without further verification. Moreover, since semantic similarity is a somewhat rough measure of mathematical relevance, the $k$-nearest neighbors of a given query can be unneccessary or miss key lemmas. Finally, Deepseek-Prover-V2 can still be prone to hallucination, for example by providing a formal proof which is entirely different from the inputted query.