neumann-prover

GitHub: https://github.com/rjain2470/neumann-prover.

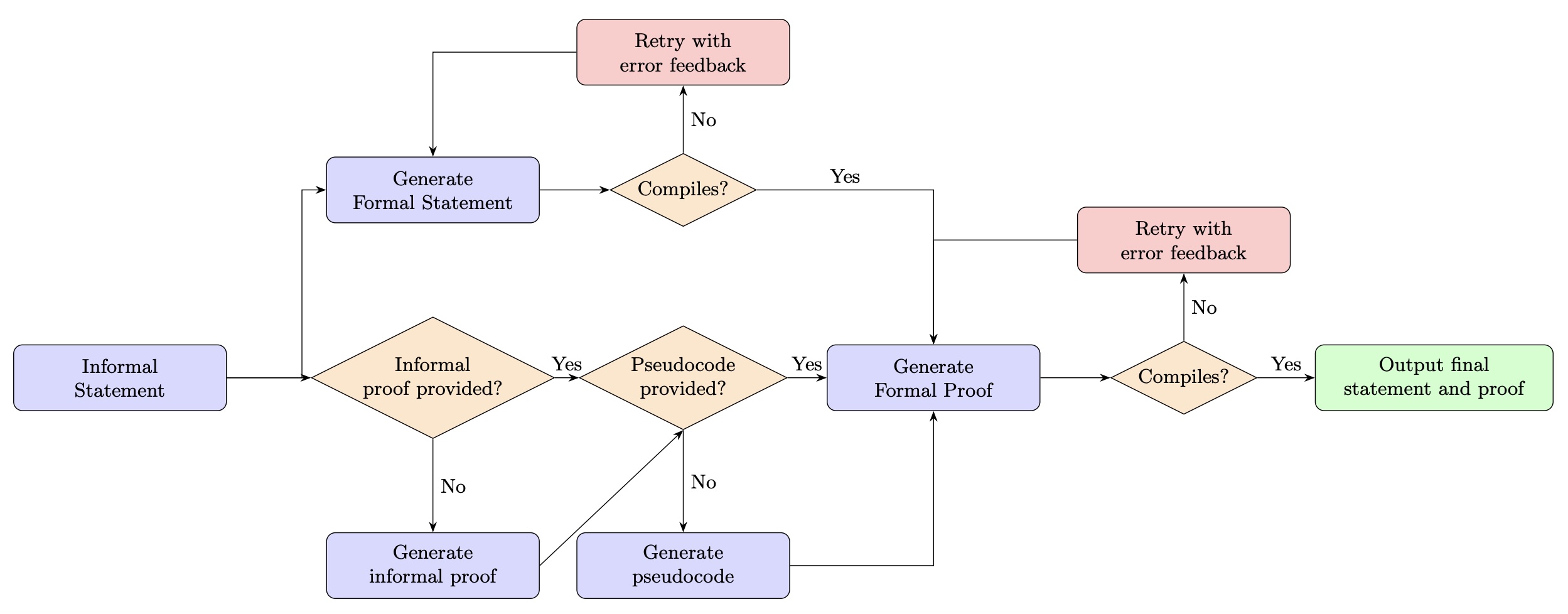
Diagram of neumann-prover’s workflow.

Neumann-prover is a multi-purpose autoformalization tool designed to produce formal proofs in Lean. It uses cutting-edge foundation models from OpenAI, and Anthropic, as well as over twenty open-source models available via Together, including offerings from DeepSeek, Qwen, and Meta. It offers extraordinary flexibility: not only can users choose which model to use, they have the option to input an informal statement and/or a formal statement in Lean, as well as the option to input an informal proof. Moreover, the user can choose whether they want (i) an informal proof, (ii) a formal statement, (iii) Lean pseudocode of a formal proof, or (iv) a formal proof. The model then interacts dynamically with the Lean compiler to iterate until it produces a correct result.

The motivation for neumann-prover stems from my experience using models trained specifically for autoformalization, such as DeepSeek-Prover-V2 and Kimina-Prover. I observed that they tended to be narrow in scope and brittle in practice, often exhibiting hallucinations in response to even minor changes in the prompt. Even worse, they often produce Lean code which compiles correctly, but prove statements which are entirely different than the one the user inputs, indicating a lack of robust semantic and reasoning capabilities.

By contrast, current foundation models exhibit strong performance in code generation and informal mathematical reasoning. Moreover, as recent work has shown, the inaccuracies in such models can effectively be mitigated through repeated attempts with structured error feedback. For instance, see the amusingly-titled paper Large Language Monkeys: Scaling Inference Compute with Repeated Sampling.

Indeed, preliminary evidence suggests that neumann-prover’s performance is quite strong, particularly in the task of autoformalization. For example, suppose we prompt the model to formalize the statement of the Stone-Weierstrass Theorem, which is as follows:

“If A is a self-adjoint algebra of bounded complex functions over a compact set X that separates points and vanishes at no point of X, then A is dense in C(X).”

First, the model generates the following rewriting of the statement, making the implicit definitions and assumptions explicit:

“Let X be a compact space and let C(X) denote the algebra of continuous complex-valued functions on X equipped with the uniform (supremum) norm. Suppose A is a subalgebra of C(X) that is closed under complex conjugation, separates the points of X (that is, for any two distinct points of X there is a function in A taking different values at those points), and does not vanish at any point of X (that is, for every x in X there exists a function in A with nonzero value at x). Then A is dense in C(X) with respect to the uniform norm; equivalently, every continuous complex-valued function on X can be uniformly approximated arbitrarily well by functions from A.”

This is highly nontrivial statement to formalize in Lean! Even still, after four attempts, neumann-prover produces the correct formalization of the theorem, which is given below.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
 
import Mathlib
namespace Demo

theorem stone_weierstrass_complex
  (X : Type*) [TopologicalSpace X] [CompactSpace X]
  (A : Set (X → Complex))
  (A_cont : ∀ f in A, Continuous f)
  (A_add : ∀ f g, f in A → g in A → f + g in A)
  (A_mul : ∀ f g, f in A → g in A → f * g in A)
  (A_smul : ∀ (c : Complex) f, f in A → (c * f) in A)
  (A*const : ∀ c : Complex, (fun * => c) in A)
  (A_conj : ∀ f, f in A → (star f) in A)
  (A_sep : ∀ x y, x ≠ y → ∃ f in A, f x ≠ f y)
  (A_nonvanish : ∀ x, ∃ f in A, f x ≠ 0) :
  ∀ (f : X → Complex), Continuous f → ∀ (eps : Real), eps > 0 → ∃ g in A, ∀ x, abs(f x - g x) < eps
:= by
  sorry

end Demo
 

While neumann-prover is still in the works, I am optimistic that the general approach of pairing foundation models with compiler-guided feedback can set a new standard for autoformalization, with promising implications for autoreasoning as well.

Limitations

The functionality of neumann-prover depends on the use of foundation models via API keys, which may become harder to obtain or more expensive to use. Moreover, foundation models may struggle to disentangle complex logical steps, failing even after multiple attempts. Additionally, neumann-prover requires a properly configured Lean and Mathlib enviroment, which can lead to setup issues as both libraries are actively evolving and subject to breaking changes. Finally, compute limitations can impact performance when handling large input batches, as the workflow involves multiple API calls and Lean code compilation processes running in parallel.